La memoria caché se sitúa entre la memoria principal y el procesador, puede estar formada por uno o varios niveles. En este apartado explicaremos el funcionamiento de la memoria caché considerando un único nivel, pero el funcionamiento es parecido si tiene varios.
La memoria caché tiene un tiempo de acceso inferior al de la memoria principal con el objetivo de reducir el tiempo de acceso medio a los datos, pero también tiene un tamaño mucho más reducido que la memoria principal. Si un dato está en la memoria caché, es posible proporcionarlo al procesador sin acceder a la memoria principal, si no, primero se lleva el dato de la memoria principal a la memoria caché y después se proporciona el dato al procesador.
Si, en la mayoría de los accesos a memoria, el dato está en la memoria caché, el tiempo de acceso medio será próximo al tiempo de acceso a la memoria caché. Eso es factible gracias a la característica de proximidad referencial de los programas.
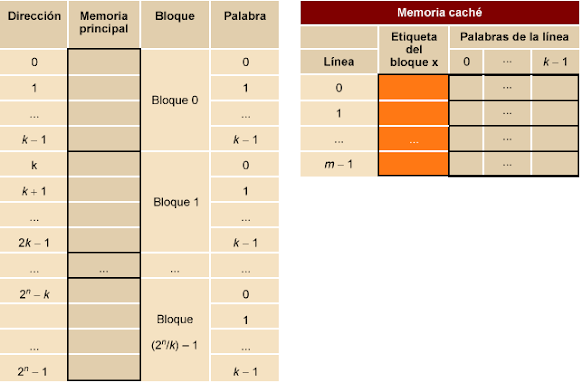
Para trabajar con memoria caché, la memoria principal se organiza en bloques de palabras, de manera que cuando hay que trasladar datos de la memoria principal a la memoria caché se lleva un bloque entero de palabras de memoria, no se trabaja con palabras individuales.
La memoria caché también se organiza en bloques que se denominan líneas. Cada línea está formada por un conjunto de palabras (el mismo número de palabras que tenga un bloque de memoria principal), más una etiqueta compuesta por unos cuantos bits. El contenido de la etiqueta permitirá saber qué bloque de la memoria principal se encuentra en cada línea de la memoria caché en un momento dado.
3.1. Aciertos y fallos.
Cada vez que el procesador quiere acceder a una palabra de memoria, primero se accede a la memoria caché; si la palabra de memoria se encuentra almacenada en la memoria caché, se proporciona al procesador y diremos que se ha producido un acierto. En caso contrario, se lleva el bloque de datos de la memoria principal que contiene la palabra de memoria hacia la memoria caché y, cuando la palabra ya está en la memoria caché, se proporciona al procesador; en este caso diremos que se ha producido un fallo.
Cuando hay un fallo, el hardware de la memoria caché debe realizar la secuencia de tareas siguiente:
1) Solicitar a la memoria principal el bloque en el que está el dato que ha producido el fallo.
2) Llevar el bloque de datos solicitado a la memoria caché. Las operaciones realizadas en esta tarea dependerán de las políticas de asignación y algoritmos de reemplazo que veremos más adelante.
3) El procesador obtiene el dato de la memoria caché como si se hubiera producido un acierto.
Un acceso con fallo en la memoria caché puede ser bastante más costoso en tiempo que un acceso con acierto, por lo que es muy importante tener un número reducido de fallos.
3.2. Rendimiento de la memoria caché.
A partir del concepto de acierto y fallo se definen los parámetros que utilizaremos para evaluar el rendimiento de una memoria caché: tasa de fallos y tiempo medio de acceso.
La tasa de fallos se define de la manera siguiente:
Tf = Número de fallos / Número de accesos a la memoria
Por otra parte se define la tasa de aciertos así:
Te = Número de aciertos / Número de accesos a la memoria = 1 – Tf
Uno de los objetivos del diseño del sistema de memoria es obtener una tasa de fallos tan baja como sea posible. Generalmente se espera que sea inferior al 10%.
Se puede calcular también el tiempo medio de acceso tm a partir de la tasa de fallos y de la tasa de aciertos, conociendo el tiempo de acceso en caso de aciertos te y el tiempo de acceso en caso de fallo tf, ya que el tiempo de fallo tiene en cuenta el tiempo necesario para llevar todo un bloque de la memoria principal a la memoria caché y el tiempo de acceso al dato.
tm = Tf x tf + Te x te = Tf x tf + (1 – Tf) x te = Tf x (tf – te) + te
Si la tasa de fallos es cero, el tiempo medio de acceso a memoria es igual al tiempo de acceso a la memoria caché.
3.3. Línea de memoria caché.
Hemos visto que la memoria caché se organiza en líneas; una línea está formada básicamente por un conjunto de palabras más una etiqueta que identifica qué bloque de la memoria principal ocupa aquella línea de la memoria caché.
La línea de memoria caché es la unidad de transferencia entre la memoria caché y la memoria principal. El tamaño de la línea es uno de los parámetros fundamentales del diseño de la memoria caché. Hay que decidir cuántas palabras se almacenarán en una línea de memoria caché, es decir, cuál es el tamaño de una línea.
Hemos visto que los datos se trasladan de la memoria principal a la memoria caché cuando hay un fallo. Si se produce un fallo, se lleva a la memoria caché el dato que lo ha provocado y el resto de los datos del bloque de memoria donde se encuentra este dato. De esta manera, se espera que los accesos siguientes sean aciertos en la memoria caché.
El tamaño de la línea es de unos cuantos bytes de información (un tamaño habitual está entre los 32 bytes y 128 bytes). Aumentar el tamaño de la línea permite aprovechar la localidad espacial, pero hasta cierto punto. Cuando se produce un fallo, el tiempo necesario para trasladar una línea más grande aumenta; además, disminuye el número de líneas disponibles de la memoria caché (el tamaño de la memoria caché es fijo) y tendremos más competencia para conseguir un bloque, lo que hará que se saquen de la caché líneas que todavía no se han utilizado en su totalidad y se reducirá el efecto de la localidad espacial, y todo ello puede representar un aumento en la tasa de fallos.
3.4. Políticas de asignación.
El número de líneas disponibles en la memoria caché es siempre mucho más pequeño que el número de bloques de memoria principal. En consecuencia, la memoria caché, además de la información almacenada, debe mantener alguna información que relacione cada posición de la memoria caché con su dirección en la memoria principal.
Para acceder a un dato se especifica la dirección en la memoria principal; a partir de esta dirección hay que verificar si el dato está en la memoria caché. Esta verificación la haremos a partir del campo etiqueta de la línea de la memoria caché que indica qué bloque de memoria principal se encuentra en cada una de las líneas de la memoria caché.
La política de asignación determina dónde podemos colocar un bloque de la memoria principal dentro de la memoria caché y condiciona cómo encontrar un dato dentro de la memoria caché.
Se definen tres políticas de asignación diferentes para almacenar datos dentro de una memoria caché:
1) Política de asignación directa: un bloque de la memoria principal solo puede estar en una única línea de la memoria caché. La memoria caché de asignación directa es la que tiene la tasa de fallos más alta, pero se utiliza mucho porque es la más barata y fácil de gestionar.
2) Política de asignación completamente asociativa: un bloque de la memoria principal puede estar en cualquier línea de la memoria caché. La memoria caché completamente asociativa es la que tiene la tasa de fallos más baja. No obstante, no se suele utilizar porque es la más cara y compleja de gestionar.
3) Política de asignación asociativa por conjuntos: un bloque de la memoria principal puede estar en un subconjunto de las líneas de la memoria caché, pero dentro del subconjunto puede encontrarse en cualquier posición.
La memoria caché asociativa por conjuntos es una combinación de la memoria caché de asignación completamente asociativa y la memoria caché de asignación directa. El número de elementos de cada subconjunto no suele ser muy grande, un número habitual de elementos es entre 4 y 64. Si el número de elementos del subconjunto es n, la memoria caché se denomina n-asociativa.
Líneas de la memoria caché donde podemos asignar el bloque x según las diferentes políticas de asignación
3.4.1. Memoria caché de asignación directa.
Para utilizar este tipo de memoria caché, se asigna cada bloque de la memoria principal a una única línea de la memoria caché.
Para relacionar una línea de la memoria caché con un bloque de la memoria principal a partir de la dirección especificada para acceder a una palabra de la memoria principal, hemos de determinar a qué bloque pertenece la dirección. Se divide la dirección en dos partes: número de bloque, que corresponde a la parte más significativa de la dirección, y número de palabra, que corresponde a la parte menos significativa.
Si tenemos una memoria principal de 2n palabras y una memoria caché de 2m líneas de 2k palabras por línea, la memoria principal se dividirá en bloques de 2k palabras. Una dirección de memoria estará formada por n bits, utilizará los k bits menos significativos para el número de palabra y los n – k bits restantes para el número de bloque.
Aclaración
No es necesario que el número de líneas de la caché sea una potencia de 2. A pesar de que habitualmente lo es, puede ser un valor donde: 2(m–1) < núm. líneas < 2(m), y utilizaremos m bits para codificar el número de línea.
Por ejemplo: si tenemos una caché de 5 líneas (22 < 5 < 23), codificaremos el número de línea utilizando 3 bits para el número de línea.
Cálculo del número de bloque
A partir de una dirección de memoria a se puede calcular el número de bloque b realizando la operación siguiente: b = a div 2k, donde div es la división entera.
El número de palabra p se puede calcular mediante la operación siguiente: p = a mod 2k, donde mod es el residuo de la división entera.
Para determinar a qué línea de la memoria caché podemos asignar cada bloque, hay que dividir el número de bloque en dos partes: una etiqueta, que corresponde a la parte más significativa del número de bloque, y un número de línea, que corresponde a la parte menos significativa.
Si tenemos un número de bloque que utiliza n – k bits, de estos n – k bits utilizaremos m bits para especificar el número de línea y el resto de los bits (n – k – m) para especificar la etiqueta.
Cálculo del número de etiqueta
A partir del número de bloque b se puede calcular la etiqueta e haciendo la operación siguiente: e = b div 2m, donde div es la división entera.
El número de línea l se puede calcular realizando la operación siguiente: l = b mod 2m, donde mod es el residuo de la división entera.
Tenemos 2n – k bloques en la memoria principal y 2m líneas en la memoria caché (2n – k > 2m), por lo tanto a cada línea de la memoria caché podemos asignar 2n – k – m (= 2n – k / 2m) bloques diferentes. Solo uno de estos 2n – k – m puede estar en la memoria caché en cada momento.
El número de línea indicará en cuál de las 2m líneas de la memoria caché se puede encontrar el bloque de datos al que queremos acceder de la memoria principal. La etiqueta nos permitirá saber si el bloque al que queremos acceder de la memoria principal es el bloque que en este momento está almacenado en aquella línea de la memoria caché.
Cuando se lleva un bloque de la memoria principal a la línea correspondiente de la memoria caché, el número de la etiqueta del bloque se almacena en el campo etiqueta de la línea, así podremos saber cuál de los 2n – k – m bloques está almacenado en esta línea de la caché. El campo etiqueta es el que nos permite identificar de manera única cada uno de los bloques que podemos asignar a una misma línea de la memoria caché.
De manera general, se puede decir que si tenemos una memoria caché de 2m líneas, los bloques de memoria principal que se pueden encontrar en cada una de las líneas de la memoria caché son los que se muestran en la tabla siguiente.
3.4.2. Memoria caché completamente asociativa.
Un bloque de la memoria principal puede encontrarse en un único conjunto de líneas de la memoria caché, pero dentro del conjunto puede encontrarse en cualquier línea.
Para relacionar una línea de la memoria caché con un bloque de la memoria principal a partir de la dirección especificada para acceder a una palabra de la memoria principal, hemos de determinar a qué bloque pertenece la dirección. Se divide la dirección en dos partes: número de bloque que corresponde a la parte más significativa de la dirección y número de palabra que corresponde a la parte menos significativa.
Si tenemos una memoria principal de 2n palabras y una memoria caché de 2m líneas de 2k palabras por línea, la memoria principal se dividirá en bloques de 2k palabras. Una dirección de memoria estará formada por n bits, utilizará los k bits menos significativos para el número de palabra y los n – k bits restantes para el número de bloque.
Cálculo del número de bloque
A partir de una dirección de memoria a se puede calcular el número de bloque b haciendo la operación siguiente: b = a div2k, donde div es la división entera.
El número de palabra p se puede calcular mediante la operación siguiente: p = a mod 2k, donde mod es el residuo de la división entera.
3.4.3. Memoria caché asociativa por conjuntos.
Un bloque de la memoria principal puede encontrarse en un único conjunto de líneas de la memoria caché, pero dentro del conjunto puede encontrarse en cualquier línea.
Para relacionar una línea de la memoria caché con un bloque de la memoria principal a partir de la dirección especificada para acceder a una palabra de la memoria principal, hemos de determinar a qué bloque pertenece la dirección. Se divide la dirección en dos partes: número de bloque que corresponde a la parte más significativa de la dirección y número de palabra que corresponde a la parte menos significativa.
Si tenemos una memoria principal de 2n palabras y una memoria caché de 2m líneas de 2k palabras por línea, la memoria principal se dividirá en bloques de 2k palabras. Una dirección de memoria estará formada por n bits, utilizará los k bits menos significativos para el número de palabra y los n – k bits restantes para el número de bloque.
Cálculo del número de bloque
A partir de una dirección de memoria a se puede calcular el número de bloque b haciendo la operación siguiente: b = a div2k, donde div es la división entera.
El número de palabra p se puede calcular mediante la operación siguiente: p = a mod 2k, donde mod es el residuo de la división entera.
Ejemplo
Si tenemos una memoria principal de 216 (64 K) palabras y una memoria caché de 210 (1.024) palabras organizada en 26 (64) líneas de 24 (16) palabras por línea, dividimos las líneas de la caché en 24 (16) conjuntos de 22 (4) líneas; por lo tanto, tendremos ω = 4 y diremos que es una memoria caché 4-asociativa.
La memoria principal se dividirá en bloques de 24 (16) palabras. Una dirección de memoria tendrá 16 bits, los 4 bits menos significativos para el número de palabra y los 16 – 4 = 12 bits restantes para el número de bloque, en total tendremos 212 (4.096) bloques de 24 (16) palabras. Las direcciones se dividirán de la manera siguiente:
El número de bloque de 12 bits se divide en etiqueta y número de conjunto: 4 bits para el número de conjunto, ya que hay 24 conjuntos, y 12 – 4 = 8 bits para la etiqueta. Así las direcciones de memoria principal se dividirán de la manera siguiente:
La asignación de bloques de la memoria principal a la memoria caché sería de la manera siguiente:
Líneas | Número de conjunto | Bloques asignados |
|---|---|---|
0, 1, 2, 3 | 0 | 0, 16, 32, 48, 64, ..., 4080 |
4, 5, 6, 7 | 1 | 1, 17, 33, 49, 65, ..., 4081 |
... | ... | ... |
60, 61,62, 63 | 15 | 15, 31, 47, 63, 79, ..., 4095 |
El mapa de direcciones de la memoria principal quedaría de la manera siguiente:
A continuación se muestra un posible contenido de la memoria caché:
A continuación se muestra la descomposición de una de las direcciones del bloque 1008 que se encuentra en la memoria caché.
3.5. Algoritmos de reemplazo.
Cuando se produce un fallo y se tiene que llevar a la memoria caché un bloque de memoria principal determinado, si este bloque de memoria se puede almacenar en más de una línea de la memoria caché, hay que decidir en qué línea de todas las posibles se pone, y sobreescribir los datos que se encuentran en aquella línea. El algoritmo de reemplazo se encarga de esta tarea.
En una memoria caché directa no es necesario ningún algoritmo de reemplazo, ya que un bloque solo puede ocupar una única línea dentro de la memoria caché. En una memoria caché completamente asociativa, solo se aplica el algoritmo de reemplazo para seleccionar una de las líneas de la memoria caché. En una memoria caché asociativa por conjuntos, solo se aplica el algoritmo de reemplazo para seleccionar una línea dentro de un conjunto concreto.
Para que estos algoritmos de reemplazo no penalicen el tiempo medio de acceso a memoria, se deben implementar en hardware y, por lo tanto, no deberían ser muy complejos.
A continuación se describen de manera general los algoritmos de reemplazo más comunes, pero se pueden encontrar otros algoritmos o variantes de estos.
1) FIFO (first in first out). Para elegir la línea se utiliza una cola, de manera que la línea que hace más tiempo que está almacenada en la memoria caché será la reemplazada. Este algoritmo puede reducir el rendimiento de la memoria caché porque la línea que se encuentra almacenada en la memoria caché desde hace más tiempo no tiene que ser necesariamente la que se utilice menos.
Se puede implementar fácilmente utilizando técnicas de buffers circulares (o round-robin): cada vez que se debe sustituir una línea se utiliza la línea del buffer siguiente, y cuando se llega a la última, se vuelve a empezar desde el principio.
2) LFU (least frequently used). En este algoritmo se elige la línea que hemos utilizado menos veces.
Se puede implementar añadiendo un contador del número de accesos a cada línea de la memoria caché.
3) LRU (least recently used). Este algoritmo elige la línea que hace más tiempo que no se utiliza. Es el algoritmo más eficiente, pero el más difícil de implementar, especialmente si hay que elegir entre muchas líneas. Se utiliza habitualmente en memorias caché asociativas por conjuntos, con conjuntos pequeños de 2 o 4 líneas.
Para memorias cachés 2-asociativas, se puede implementar añadiendo un bit en cada línea; cuando se hace referencia a una de las dos líneas, este bit se pone a 1 y el otro se pone a 0 para indicar cuál de las dos líneas ha sido la última que se ha utilizado.
4) Aleatorio. Los algoritmos anteriores se basan en factores relacionados con la utilización de las líneas de la caché; en cambio, este algoritmo elige la línea que se debe reemplazar al azar. Este algoritmo es muy simple y se ha demostrado que tiene un rendimiento solo ligeramente inferior a los algoritmos que tienen en cuenta factores de utilización de las líneas.
3.6. Comparativa entre diferentes sistemas de memoria caché.
Utilizaremos un ejemplo para ver cómo los accesos a memoria de un programa pueden producir aciertos y fallos en la memoria caché y cómo modifican el contenido de la memoria caché.
Supongamos una memoria principal de 210 (1.024) palabras, en la que cada dirección de memoria corresponde a una palabra, y una memoria caché de 24 (4) líneas de 22 (4) palabras; por lo tanto, la memoria principal también estará organizada en bloques de tamaño de 4 palabras.
Para determinar el número de bloque que corresponde a una dirección de memoria, dividimos la dirección d entre el número de palabras de un bloque:
b = d div 2k = d div 4
Este número de bloque se aplica a todas las organizaciones de la memoria caché.
3.6.1. Memoria caché de asignación directa.
En una memoria caché directa un bloque de memoria solo se puede encontrar en una única línea de la memoria caché. A un bloque de memoria b le corresponderá la etiqueta e y lo asignaremos a la línea l de la memoria caché, para determinar la etiqueta y la línea, dividimos el número de bloque b entre el número de líneas de la memoria caché:
e = b div 2m = b div 4
l = b mod 2m = b mod 4
3.6.2. Memoria caché completamente asociativa.
Utilizamos ahora una memoria caché completamente asociativa. En una memoria caché completamente asociativa, un bloque de memoria principal se puede encontrar en cualquier línea de la caché. Las direcciones de memoria se dividen en número de bloque y número de palabra.
Mostramos los primeros 16 bloques de la memoria principal con las direcciones de memoria que contiene el bloque:
b (a0 ,a1 ,a2 ,a3): bloque (direcciones del bloque) | |||
0 (0,1,2,3) | 4 (16,17,18,19) | 8 (32,33,34,35) | 12 (48,49,50,51) |
1 (4,5,6,7) | 5 (20,21,22,23) | 9 (36,37,38,39) | 13 (52,53,54,55) |
2 (8,9,10,11) | 6 (24,25,26,27) | 10 (40,41,42,43) | 14 (56,57,58,59) |
3 (12,13,14,15) | 7 (28,29,30,31) | 11 (44,45,46,47) | 15 (60,61,62,63) |
Cabe remarcar que el número de bloque es el número de etiqueta que tendremos almacenado en la memoria caché.
3.6.3. Memoria caché asociativa por conjuntos.
En una memoria caché asociativa por conjuntos con dos conjuntos de dos líneas, un bloque de memoria se puede encontrar en un único conjunto y dentro del conjunto en cualquier línea. A un bloque de memoria b le corresponderá la etiqueta e y lo asignaremos al conjunto j de la memoria caché, para determinar la etiqueta y el conjunto, dividimos el número de bloque b entre el número de líneas de cada conjunto:
e = b div 2c = b div 2
j = b mod 2c = b mod 2
Por lo tanto, los bloques de memoria principal que se pueden asignar a cada conjunto de la memoria caché son los siguientes:
j: número de conjunto | Línea | Bloques | Bloque: etiqueta (7 bits) conjunto de 1 bit |
|---|---|---|---|
0 | 0 | 0, 2, 4, 6, 8, ..., 254 | 0:0(0000000) 0, 2:1(0000001) 0, 4:2(0000010) 0, ..., 254:127(1111111) 0 |
1 | |||
1 | 2 | 1, 3, 5, 7, 9, ..., 255 | 1:0(0000000) 1, 3:1(0000001) 1, 5:2(0000010) 1, ..., 255:127(1111111) 1 |
3 |
Mostramos a qué conjuntos de la memoria caché se asignan los primeros 16 bloques de memoria principal con las direcciones de memoria que contiene el bloque:
j: número de conjunto | b:e (a0 ,a1 ,a2 ,a3): bloque asignado : etiqueta (direcciones del bloque) | |||
|---|---|---|---|---|
0 | 0:0 (0,1,2,3) 2:1 (8,9,10,11) | 4:2 (16,17,18,19) 6:3 (24,25,26,27) | 8:4 (32,33,34,35) 10:5 (40,41,42,43) | 12:6 (48,49,50,51) 14:7 (56,57,58,59) |
1 | 1:0 (4,5,6,7) 3:1 (12,13,14,15) | 5:2 (20,21,22,23) 7:3 (28,29,30,31) | 9:4 (36,37,38,39) 11:5 (44,45,46,47) | 13:6 (52,53,54,55) 15:7 (60,61,62,63) |
Hay que remarcar que especificamos el número de bloque y el número de etiqueta, pero que el valor que tendremos realmente almacenado en la caché es tan solo la etiqueta asociada al bloque.
3.7. Políticas de escritura.
Cuando accedemos a la memoria caché, podemos hacer lecturas o escrituras; hasta ahora hemos visto la problemática de acceder a la memoria caché para leer un dato. Cuando se debe realizar una operación de escritura, aparecen nuevos problemas porque los datos que tenemos en la memoria caché son una copia de los datos que tenemos en la memoria principal y hay que garantizar la coherencia de los datos.
Analizaremos el caso con un único procesador y un único nivel de memoria caché entre el procesador y la memoria principal. Si tenemos más de un procesador con una memoria caché local para cada procesador, la modificación de un dato en una de estas memorias caché invalida el valor del dato en la memoria principal, pero también invalida el valor del dato si se encuentra en otra memoria caché. De manera parecida, si tenemos otros dispositivos que puedan modificar directamente un dato de la memoria principal, el valor de este dato queda invalidado en las memorias caché donde se pueda encontrar. La gestión de la coherencia en estos sistemas es más compleja y no se analizará aquí.
A continuación comentaremos diferentes políticas para gestionar las escrituras y mantener la coherencia entre los datos de la memoria caché y la memoria principal:
1) Escritura inmediata (write trough): cuando se escribe en la memoria caché, también se escribe en la memoria principal transfiriendo todo el bloque que contiene el dato modificado; de esta manera en todo momento la copia que tenemos en la caché es idéntica a la que tenemos en la memoria principal. La política de escritura inmediata es la más fácil de implementar, pero su inconveniente es que produce un gran flujo de información entre la memoria caché y la memoria principal.
2) Escritura aplazada (write back): las escrituras se efectúan solo sobre la memoria caché. La memoria principal se actualiza cuando se elimina una línea de la memoria caché que ha sido modificada. Eso implica añadir algunos bits a cada línea de la memoria caché para saber si la línea se ha modificado o no.
Si hay que reemplazar una línea que ha sido modificada, primero es necesario copiar la línea modificada a la memoria principal y a continuación llevar el nuevo bloque, lo que aumenta significativamente el tiempo para acceder al dato.
Fallo en la escritura
Cuando se quiere hacer una escritura de una dirección que no está en la memoria caché, se producirá un fallo; este fallo se puede tratar de diferentes maneras:
a) Escribir directamente en memoria principal y no llevar el dato a la memoria caché. Esta técnica se puede utilizar en la escritura inmediata. Evitamos transferir el bloque a la caché pero no se tiene en cuenta la proximidad referencial, ya que es muy probable que haya nuevos accesos al mismo bloque de datos.
b) Llevar el bloque a la memoria caché y escribir simultáneamente en la caché y en la memoria principal. Esta técnica es la que se utiliza habitualmente en la escritura inmediata.
c) Llevar el bloque a la memoria caché y escribir solo en la caché. Esta técnica se utiliza habitualmente en escritura aplazada.
En máquinas reales se utilizan cada vez más políticas de escritura aplazada, pero el tratamiento de los fallos en caso de escritura es diferente, principalmente porque se consideran diferentes niveles de memoria caché y porque múltiples dispositivos (procesadores, DMA, canales de E/S) pueden acceder a la memoria.
0 Comentarios